
Background
Many recent works have shown that organic matrices employed to produce composite materials are hydrophilic. It is thus of first importance to study the moisture diffusion process within these materials since it leads to a significant drop of the mechanical properties and to relevant internal mechanical states. Those high internal stresses may then favor the material damage leading, for instance, to crack propagations within the matrix. Moreover, the complex physic of the problem is submitted to significant uncertainties which should be taken into account when one seeks robust predictions. The FIRMAIN project aims at linking recent and efficient numerical approaches in order to study the coupling between water diffusion and damage; the proposed techniques will be extended to the stochastic framework.
Scientific advances and innovation
Water diffusion in composites has already been widely studied by many international research teams which tend to say that its impact is harmful for the material. However, even if experimental results exist, we do not find efficient numerical methods associated to relevant models which allow predicting the behavior of the structure. The FIRMAIN project will lead to significant advances on the development of models and numerical techniques. Besides, all proposed tools will be extended to the stochastic framework so that uncertainties on physical phenomena, geometry, and crack paths can be taken into account. Such approaches will enable to characterize in a probabilistic manner, with statistical information and/or probability laws, critical quantities of interest used in the design of MRE structures. They will also permit a better understanding of coupling between moisture diffusion and composites damage.
Expected technical and economic impact
Marine Renewable Energy structures are from now on widely made of organic matrix based composites which possess excellent mechanical properties but which may be damage by various attacks from marine environment. The aim of the FIRMAIN project is to develop numerical tools for engineers which will allow studying the influence of water diffusion within the composites on the material damage. These tools will allow optimizing the lifespan of MRE structures and reducing the cost of the energy produced.
Key project milestones
- October 2016 - Project beginning
- October 2017 - Bibliographic report and development of deterministic coupled model
- October 2018 - Development of deterministic coupled model and extension of uncoupled models to the stochastic framework
- June 2020 - Development of stochastic coupled model, thesis defense and papers in international journals
Demonstrator
Development of numerical tools in order to analyze the damage of composite materials employed in Marine Renewable Energy structures.
Results
Experimental campaign on the damage of composites damage used in MRE structures in humid environment :
The experimental campaign aimed at studying the hygroscopic behavior of glass/epoxy composite samples at various damage levels. To achieve this task, a protocol was set up and a dedicated climatic chamber was designed and built (see figure 1-left). Among the obtained results, we found that the damage level modified the hygroscopic behavior (diffusion speed and maximum absorption capacity) as shown on figure 1-right. Both diffusion coefficients and maximum absorption capacities were identified using a search algorithm developed under the Matlab© software.
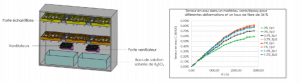
Figure 1: (left) CAD model of the chamber for aging and (right) sorption curves obtained for composite samples corresponding to different damage levels.
The study showed that those parameters were increasing with the damage level: presence of cracks influences the diffusion coefficient while the increase of the maximum absorption capacity seems mode likely be due to the formation of porosities (see figure 2).

Figure 2: (left) SEM observation with crack and (right) SEM observation of porosity done for glass/epoxy samples from the project.
Deterministic and stochastic hygroscopic models with crack at the micro-scale:
This first numerical work aimed setting up the hygroscopic model which takes into account the so-called “oulet” edge cracks through which the water diffusion can take place. Solving this type of problem required the implementation of dedicated numerical methods. In order to overcome the particular problem of remeshing, the method of the extended finite elements (X-FEM) was retained and adapted to the specificities of the problem by using a technique of penalty and functions of enrichment allowing imposing a water content as boundary conditions along the crack and thus capture irregularities in the solution across the crack front. Figure 3 presents illustrations of the water content fields of a glass/epoxy composite during the transient part of the process for cases with and without crack. One can see that the water diffusion within the material is much more advanced for the case with a crack. Figure 4 presents a comparison of sorption curves (evolution of the global water content over time) for these same two cases. We can observe a much faster diffusion in the case with crack.
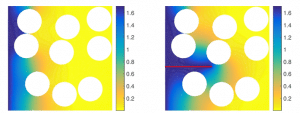
Figure 3: comparison of the water content fields [% H20] for a glass/epoxy composite without crack (left) and with crack (right).
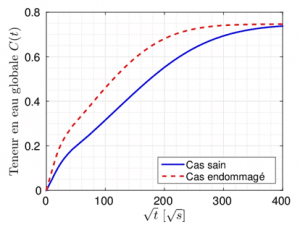
Figure 4: sorption curves obtained by simulation for a healthy case (without crack) and a damaged case (with crack).
The problem was then extended to the stochastic framework through probabilistic modeling in which the variability is represented by a finite set of random variables. The propagation of uncertainties, consisting in determining the uncertainties at the output of the model as a function of the input uncertainties, is carried out using stochastic spectral approaches consisting in finding the solution in a functional form. This type of method is effective when the number of input random variables is relatively low. The proposed approach has been the subject of specific developments in order to adapt to the hygroscopic framework of this work. Examples of results are given in Figures 5 and 6. In this problem both crack length and maximum absorption capacity are represented using random variables. The randomness on the crack length was chosen to be high (coefficient of variation of 45%) as often observed, while the one related to the maximum absorption capacity is significantly lower (coefficient of variation of 5%). Figure 3 shows the random sorption curve of the problem using its mean and a 95% confidence interval. On the same figure is illustrated the response surface of this random process at a given time where the dispersion is significant.
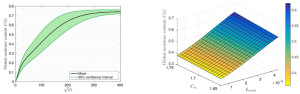
Figure 5: random sorption curve (left) and characteristic response surface at a given time (right).
It can be observed that the variability on the crack length has a much greater impact than the variability on the maximum absorption capacity. Figure 6 shows a post-processing of the stochastic solution leading to a rapid evaluation of water content fields for different random realizations of crack length and maximum absorption capacity. It can be seen that, as previously, the larger the crack is, the more advanced the water diffusion is.
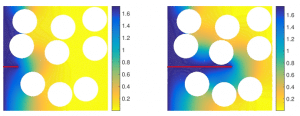
Figure 6: examples of local water content fields for two lengths of cracks obtained by post-processing of the stochastic solution.
The proposed approach also allows determining the evolution of the effective diffusion coefficient as a function of the crack length by considering the spatial studying doamin as a representative elementary volume. Two cases were studied: the case of an epoxy resin alone in the presence of a crack and the case of a glass/epoxy composite also in the presence of a crack. Figure 5 illustrates the results for these two cases. We can observe a significant increase in this effective diffusion coefficient in both cases. This type of result can be used in design simulations at higher scale when one want to assess the damage effect on the water diffusion.
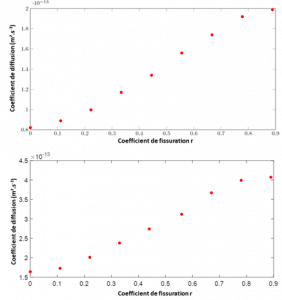
Figure 5: evolution of the apparent diffusion coefficient as a function of the crack length ratio (close to a crack density) for a neat epoxy resin (left) and a glass epoxy composite (right).
Deterministic and stochastic hygro-elastic models with crack at the micro-scale:
In this part, the objective was to take into account the hygroscopic strain resulting from the water diffusion in the elastic computations. To do so, the X-FEM method was adapted in order to take into account the results from the hygroscopic computations (local water content) illustrated in the previous part. The following illustrations come from a stochastic study on the same glass/epoxy composite with the same properties. Figure 6 shows the evolution of the maximum random vertical stress as well as its response surface as a function of the crack length and the maximum absorption capacity. Figure 7 shows the same types of results for the opening of the crack. In both cases, we can observe a significant variability in the results mainly coming from the randomness related to the length of the crack.
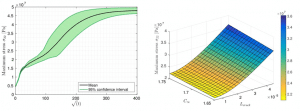
Figure 6: evolution of the maximum random vertical stress (left) and characteristic response surface at a given time (right).
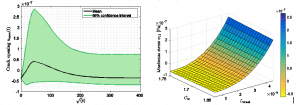
Figure 7: evolution of the random crack opening (left) and characteristic response surface at a given time (right).
Deterministic and stochastic hygro-elastic models with crack propagation at the micro-scale:
In this last part, we have improved the proposed model to take into account the propagation of a crack during aging. A deterministic study was proposed in order to compare a hygro-elastic computation with and without crack propagation. Figure 8 shows the evolution of the water content field as a function of the crack propagation resulting from the diffusion of water within the glass/epoxy composite material.
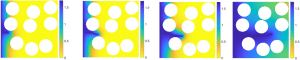
Figure 8: evolution of the water content field with respect to the crack propagation.
Figure 9 presents comparisons between computations without crack propagation and with crack propagation. First of all, it can be seen that the global water content is very much affected by crack propagation with a higher diffusion rate and saturation reached earlier than in the case without crack propagation. Moreover, one can observe on figure 9-right a much larger and faster crack opening for the case with crack propagation.
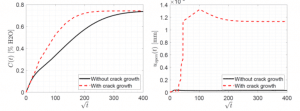
Figure 9: comparison between cases without crack propagation and with crack propagation: (left) comparison of the evolution of the global water content and (right) evolution of the maximum crack opening.
Finally, we have proposed a stochastic study of the behavior of the parameters controlling the crack propagation: the angle of propagation of the crack and the increase in its length in particular. Figures 10 and 11 present some stochastic results, in the form of stochastic processes and characteristic response surfaces, for these 2 quantities, considering the length of the crack as well as the maximum absorption capacity as random variables.
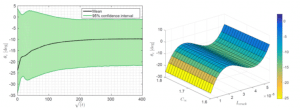
Figure 10: evolution of the crack propagation angle θC: (left) stochastic process with mean and confidence interval and (right) characteristic response surface as a function of the length of the crack Lcrack and the maximum absorption capacity C∞.
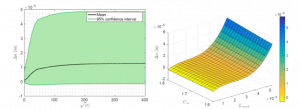
Figure 11: evolution of the increase in crack length Δa: (left) stochastic process with mean and confidence interval and (right) characteristic response surface as a function of the length of the crack Lcrack and the maximum absorption capacity C∞.
On each one of these last two figures, we can observe a significant variability as indicated by the very wide confidence intervals. A slight distinction should however be noted: indeed, as the response surfaces show, this variability comes almost exclusively from the hazard over the length of the crack for the angle of propagation while the maximum absorption capacity plays a significant role in the variability of the increase in crack length.
Publications and papers published
Oral communications
- Stochastic study of the hygro-elastic behavior of composite materials: application to the durability of renewable marine energy structures, Clément, A., Bhati, G., Fréour, S. et Jacquemin, F. , 54th ESReDA Seminar on Risk, Reliability and Safety of Energy Systems In Coastal and Marine Environments, April 25 – 26, Nantes. (2018).
- Multiphysics modeling of the hygro-mechanical behavior of composites used in Marine Renewable Energy structures, A. Clément, A. Uguen, Q. Dézulier, S. Fréour, F. Jacquemin (GeM, Research Institute in Civil and Mechanical Engineering, CNRS UMR 6183, Nantes University, Centrale Nantes, France) – French American Innovation Day 2019 – Download the poster
- Study of the hygro-elastic behavior of composite materials in presence of cracks: application to the durability of renewable marine energy structures, A. UGUEN, A. CLEMENT, S. FREOUR, F. JACQUEMIN, European Mechanics Society Colloquium 607 on Marine Aging of Polymers, Brest France, August 28th-29th 2019.
- Characterization and modelling of coupled hygro-thermo-mechanical behaviour of composites in harsh environment, A. CLEMENT, OPIN Workshop, Advanced Materials and Manufacturing (composite focus), 12 Novembre 2019, technocpaus OCEAN, Bouguenais – France.
- Numerical stochastic study of damaged composite materials in humid environment, A. CLEMENT, S. FREOUR, F. JACQUEMIN. JOINT EVENT: ICCS23 – 23rd International Conference on Composite Structures & MECHCOMP6 – 6th International Conference on Mechanics of Composites, 1-4 septembre 2020, Université de Porto, Portugal.






