Background
This work was carried out within the framework of the WEAMEC – FIRMAIN project – and with funding from the CARENE.
Abstract
The present work is devoted to the durability of composite materials used in MRE structures submitted to harsh environments. Many recent works have indeed shown that organic matrices employed to produce composite materials are hydrophilic. It is thus of first importance to study the moisture diffusion process within these materials since it leads to a significant drop of the mechanical properties and to relevant internal mechanical states coming from the hygroscopic swelling of the hydrophilic matrix.
This work aims at studying the impact of hygroscopic aging on crack propagation submitted to uncertainties in composite materials. Indeed, water diffusion in composites has already been widely studied by many international research teams which tend to say that its impact is harmful for the material. However, even if experimental results exist, we do not find efficient numerical methods associated to relevant models which allow predicting the behavior of the structure.
In this work, we propose an extended finite element method (X-FEM) formulation for the hygro-mechanical problem involving existing crack to study its propagation when moisture diffusion occurs. Based on an implicit representation of the geometry (the crack for instance) with the level-sets technique and on enrichment approximation strategies based on prior physical knowledge, this numerical approach allows using arbitrary finite element meshes and thus avoids remeshings during the computation.
Moreover, the complex physic of the problem is submitted to significant uncertainties which should be taken into account when one seeks robust predictions. To achieve this task, we propose an extension of the proposed method to the stochastic framework using spectral approaches such as polynomial chaos approximation. These methods are good candidates in order to get an explicit solution with respect to the basic random variables modeling the diffusion coefficients or the crack length, for instance. They consist in representing the random solution on a suitable approximation basis.
Variability related to physical parameters, loadings or geometry can thus be taken into account in the computations. The use of the extended finite element greatly helps dealing with geometrical uncertainties in a parametric/stochastic way since the geometry does not have to be conformed to the finite element mesh.
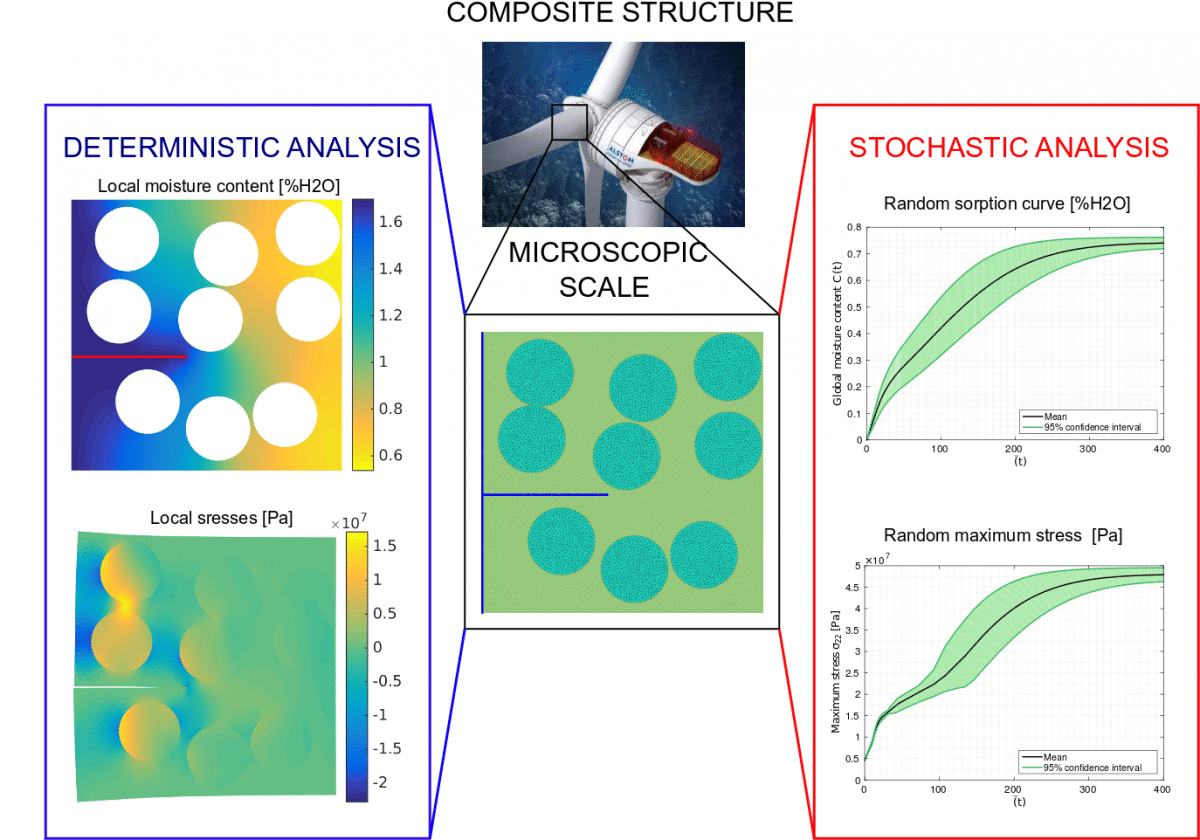
Numerical studies involving homogeneous and heterogeneous materials will allow showing the efficiency of the technique and the impact of cracks on the diffusion behavior. As an example figure 1 illustrates deterministic and stochastic analyses for a microscopic hygro-mechanical problem. In this study, we consider an elementary volume of an epoxy/glass composite with an edge crack from which moisture can diffuse within the materials. The length of the crack and the maximum water capacity are modelled with random variable. On the left side, we have depicted typical deterministic results (local moisture content and stress fields) for a particular time and a given realization of the random variables. On the right side of the same figure, we show some stochastic results on the sorption curve and the maximum local stress for which the confidence interval in green indicates a significant variability related to the input uncertainties.

