OMCEND

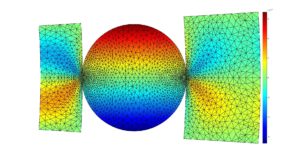
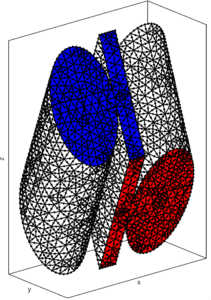
L’approche développée dans le cadre du projet pour la modélisation d’une armure simple (câble statique) combine deux méthodes. D’une part, nous utilisons une méthode numérique bidimensionelle spécifique, qui préserve la description analytique du problème selon une troisième direction, celle de propagation et qui est hélicoïdale. Cette méthode permet de prendre en compte la symétrie hélicoïdale continue de l’armure et de ses gaines environnantes. D’autre part, nous avons utilisé la théorie des milieux périodiques pour prendre en compte la symétrie de rotation discrète de la section de l’armure. La prise en compte de ces deux types de symétrie dans les modèles permet de réduire considérablement la taille des problèmes à résoudre sans faire la moindre approximation (réduction d’un facteur supérieur à 1000 par rapport à un modèle 3D complet). À titre indicatif, on peut passer successivement d’un nombre de degrés de liberté (taille des matrices impliquées dans les résolutions numériques) de l’ordre de deux milliards en 3D (Figure 2 à gauche), à un million en 2D (Figure 2 à droite), puis finalement à seulement 20 000 par symétrie de rotation (Figure 3 à gauche). Ceci permet d’accéder à des ondes hautes fréquences, nécessaires à toute technique d’évaluation non destructive par ondes guidées. Les modélisations tiennent compte des effets du contact brins-gaines et des pertes viscoélastiques dans les matériaux.

Figure 2 : modèle 3D d’une armure simple (à gauche) et sa section 2D (à droite).

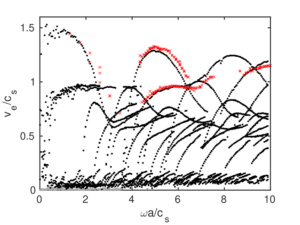
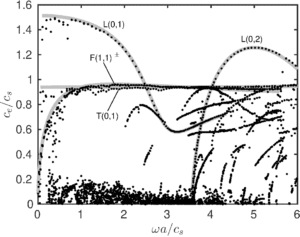
Le modèle d’armure simple permet de calculer aussi bien les champs liés aux chargements statiques appliqués (pression externe, élongation, …) que les courbes de dispersion des modes d’onde (vitesse des ondes, atténuation, …) – voir Figure 3. Le modèle a pu être validé numériquement et expérimentalement. Les simulations permettent en particulier d’estimer les distances de propagation des ondes, dont la connaissance est cruciale pour évaluer la faisabilité des techniques d’END à base d’ondes guidées.

Figure 3 : résultats numériques pour une armure simple. À gauche : maillage de la cellule unitaire du problème et champ microscopique du déplacement axial statique. À droite : courbes normalisées de vitesse d’énergie en fonction de la fréquence des modes d’onde. Croix rouges : résultats expérimentaux.

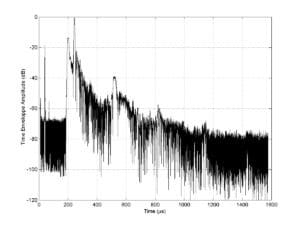
Les résultats expérimentaux obtenus sur des échantillons comportant un défaut de type fil rompu confirment les tendances des résultats numériques, à savoir que les modes les plus attractifs pour l’END sont plutôt dans un régime basse fréquence (voir Figure 4). Deux modes potentiellement intéressants pour l’END des fils d’armure ont pu être identifiés : le mode L(0,3) autour de 1.3MHz, d’atténuation de l’ordre de 30dB (soit une distance de propagation de 2 à 3m), et le mode L(0,1), qui est le mode le moins atténué, avec une atténuation de l’ordre de 15dB autour de 400kHz (soit une distance de propagation double, donc de 4 à 6m). Le mode L(0,2) présente une atténuation comparable au L(0,3) mais est moins excitable. Les modes d’ordre supérieur L(0,n) (n>3) sont, quant à eux, significativement plus atténués que les autres.

Figure 4 : signaux temporels mesurés expérimentalement en transmission dans un fil d’ombilical (excitation large bande). Les différents pics correspondent aux échos générés par les extrémités de l’échantillon. Une analyse temps-fréquence permet de montrer que les modes les plus échogènes sont les modes basse fréquence.

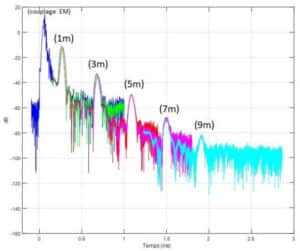
Un dispositif magnétostrictif a été mis en oeuvre. Ce dispositif présente l’intérêt d’être sans contact (encerclant localement). Son fonctionnement dans un régime basse fréquence, plus compatible avec la propagation du mode L(0,1), a permis d’augmenter la distance de propagation de ce mode jusqu’à 9m en basse fréquence (voir Figure 5). Par ailleurs, ce dispositif s’avère capable de détecter un défaut franc d’assez petite taille correspondant à un seul brin rompu sur 50 (soit une réduction de section de l’armure de 2%). Soulignons que le mode L(0,1) est un mode basse fréquence, susceptible d’avoir un comportement de nature globale impliquant une dynamique de l’ensemble de la section du câble. Ceci peut être vu comme un inconvénient si l’on vise spécifiquement l’END de l’armure, ou un avantage pour un END plus global. La nature globale ou locale du mode L(0,1) en basse fréquence est une question ouverte, que les travaux réalisés dans le cadre du projet ne permettent pas de trancher.

Figure 5 : empilement d’enveloppes des arrivées temporelles du mode L(0,1), détectées par dispositif d’émission-réception magnétostrictif dans un domaine basse fréquence.

Aucun échantillon de double armure n’a pu être mis à disposition durant le projet. Les seuls résultats obtenus sur cette structure sont donc numériques. L’approche de modélisation développée pour une armure simple n’est pas applicable dans le cas d’une armure double (câble dynamique). Ceci est dû au fait que les deux couches d’armure tournent dans des sens opposés, ce qui brise complètement la symétrie continue du problème. L’approche que nous avons développée est basée sur la théorie des milieux périodiques suivant deux directions. Pour une armure double, la cellule unitaire du problème est ainsi réduite à une cellule tridimensionnelle dont les dimensions sont de l’ordre du diamètre des brins (voir Figure 6 à gauche). Toutefois, des difficultés d’ordre théorique se posent du fait de la courbure des deux axes de périodicité (géométrie en double hélice). Dans le cadre du projet, nous avons proposé un système de coordonnées particulier, de type bi-hélicoïdal, prouvé l’existence de modes d’ondes dans une telle géométrie, puis établi les conditions de mise en œuvre numérique de notre approche. Les résultats numériques obtenus sur armure double (voir Figure 6 à droite) montrent des tendances similaires à celles observées pour une armure simple.

Figure 6 : résultats numériques pour une double armure. À gauche : réduction du maillage à la cellule unitaire répétitive du problème, à droite : courbes normalisées de vitesse d’énergie en fonction de la fréquence des modes d’onde (traits gris : cas d’un brin libre).

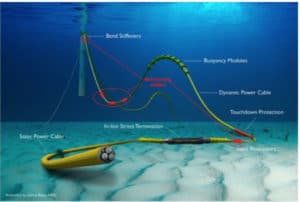
Les résultats du projet permettent d’envisager une instrumentation judicieuse pour le monitoring d’un câble dynamique. Celle-ci consisterait à concevoir des colliers magnétostrictifs d’émission-réception, placés à proximité des zones critiques d’endommagement (connecteurs, hubs,…) – voir Figure 7. Les avantages d’un dispositif magnétostrictif sont multiples. Aucun accès particulier n’est nécessaire puisqu’il peut être monté sur la gaine externe directement. Son régime de fonctionnement, relativement basse fréquence, permet au mode L(0,1) de se propager sur une dizaine de mètre. Cette distance de propagation apparaît compatible avec la taille des zones critiques. Ce type de dispositif est global. Il ne nécessite pas une instrumentation fil à fil et est donc moins coûteux et plus facile à mettre en œuvre. Le savoir-faire acquis durant le projet, en terme de méthodes de modélisation et d’expérimentation, pourra être exploité pour d’autres architectures de câbles et d’autres types de dispositifs si nécessaires.

Figure 7 : câble d’éolienne flottante. En rouge : instrumentation localisée autour de zones critiques par colliers magnétostrictifs externes.

Perspectives

Mise au point de techniques in-situ fiables et à faible coût pour le contrôle non destructif et la surveillance de l’intégrité mécanique des câbles.