ROS-3D

Objectifs :

Les travaux de ce projet concernent deux points : (i) le développement de modèles déterministes tridimensionnels efficaces pour les fondations d’éoliennes en mer soumises à des chargements axiaux et latéraux et (ii) le développement de modèles probabilistes afin de calculer la probabilité de défaillance de la fondation offshore tenant compte de la variabilité spatiale tridimensionnelle des propriétés du sol.

Méthodologies adoptées :

– Pour le développement de modèles mécaniques, une fondation offshore de type monopieu de grand diamètre a été modélisée à l’aide du logiciel d’éléments finis Abaqus. Deux types de modélisation ont été envisagés dans le modèle mécanique : un modèle ‘wished in place’ et un modèle plus sophistiqué prenant en compte le processus d’installation de la fondation. Le dernier modèle utilise l’approche eulérienne-lagrangienne couplée implémentée dans le logiciel Abaqus.

• Pour les analyses probabilistes, trois méthodes probabilistes efficaces basées sur la technique de méta-modèle de Krigeage ont été développées dans ce travail : GSAS, AK-MCSm et AK-MCSd. La méthode GSAS combine le Krigeage avec l’analyse de sensibilité globale, l’objectif étant de fournir un meilleur enrichissement du méta-modèle par rapport à l’approche classique de Krigeage. L’approche AK-MCSm utilise un enrichissement multipoint, ce qui est très utile en cas de disponibilité d’installations informatiques permettant des calculs parallèles. Enfin, l’approche AK-MCSd utilise la dépendance entre les prédictions de Krigeage et permet de réduire le temps de calcul par rapport à l’approche classique de Krigeage.

Les résultats issus des différentes simulations sont les suivants :

• Pour la détermination de la capacité portante ultime verticale, on observe une concordance de résultats entre l’approche numérique sous Abaqus et celle de l’API. La contribution de la résistance du fut et de la base du monopieu dans la résistance totale du monopieu a été déterminée. Les résultats ont montré une contribution majeure de 60-80% pour le fut et une contribution de 20-40% pour la base. En plus, il a été remarqué que le fut atteint la rupture en premier lieu. Il a été montré que le sol à l’intérieur du monopieu reste solidaire de ce monopieu lors du chargement de ce dernier. La capacité portante du monopieu se calcule donc comme étant la somme de la résistance du fut et celle de la base du monopieu (sol + anneau). Ceci est conforme avec les préconisations de l’API.

• Les résultats du monopieu de grand diamètre soumis à un chargement latéral ont montré que le monopieu subit un mouvement de rotation rigide autour d’un point situé autour du tiers inférieur de la longueur encastrée du monopieu. Les résultats issus de la modélisation du processus d’installation du monopieu dans le sable ont montré que le phénomène de bouchon (plugging phenomenon) augmente avec la diminution du diamètre du monopieu, l’augmentation de la densité du sable et l’augmentation de la force d’installation. Pour les monopiles de grand diamètre, le phénomène de bouchon s’est avéré peu probable. De plus, les résultats ont montré que l’état de contrainte autour du monopieu est significativement modifié par l’installation du monopieu. Ce changement pourrait avoir un effet significatif sur la réponse du monopieu.

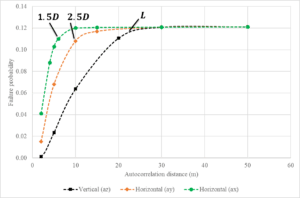
• Concernant les approches probabilistes développées, il a été démontré que ces méthodes présentent une grande efficacité en terme du temps de calcul et ce, par rapport à l’approche probabiliste classique de Monte Carlo et par rapport aux méthodes probabilistes classiques basées sur le Krigeage. La méthode AK-MCSm s’est avérée la méthode la plus efficace en terme de temps de calcul. Cependant, elle nécessite la disponibilité d’installations informatiques permettant des calculs parallèles. AK-MCSd s’est montrée plus pertinente que l’approche GSAS car elle est basée sur une méthodologie d’enrichissement plus efficace en terme du temps de calcul.D’autre part, il a été démontré que l’effet de la variabilité spatiale 1-D dans la direction verticale est très influant sur la probabilité de défaillance tant que la distance d’autocorrélation verticale est inférieure à la longueur du monopieu. En plus, il a été démontré que l’effet de la variabilité spatiale horizontale apparaît dès que la distance d’autocorrélation horizontale devient inférieure à 2.5 D où D est le diamètre du monopieu. Dans le cas d’une variabilité tridimensionnelle du sol, l’utilisation d’une méthode classique de discrétisation de champ aléatoire (par exemple EOLE) induit un problème de mémoire. Afin de résoudre ce problème, la méthode ‘Turning Band Method’ TBM a été proposée. Cette méthode s’est révélée très efficace pour la discrétisation d’un champ aléatoire tridimensionnel avec de très faibles distances d’autocorrélation (c’est-à-dire dans le cas d’un sol très hétérogène). Cependant, cette méthode présente un défaut lié au grand nombre de variables aléatoires qu’elle nécessite pour représenter un champ aléatoire. Ceci entrave sa combinaison avec une approche basée sur le Krigeage qui ne peut gérer qu’un nombre limité de variables aléatoires.

Figure : Effet de la variabilité spatiale sur la probabilité de défaillance

PRÉSENTATION DU PROJET LORS DU SÉMINAIRE WEAMEC « GÉOTECHNIQUE & GÉOPHYSIQUE POUR LES APPLICATIONS EMR »